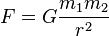Rabu, 04 November 2009

Penggunaan Operasi Integral Dan Diferensial/Turunan

Posisi (r), Kecepatan (v) dan percepatan (a) dengan penyelesaian matematis menggunakan diferensial/turunan dan integral bisa didapatkan bila salah satu variable diketahui persamaannya.

Lihat Diagram berikut !

diagram integral turunan

Bila r diketahui, maka v dan a dapat dicari dengan diferensial/turunan, demikian juga bila v diketahui a didapat dari penurunan v
Bila diketahui, maka persamaan kecepatan (v) dan posisi (r) dapat ditentukan dengan integral, demikian pula bila v diketahui, posisi dapat diselesaikan.

RUMUS DIFERENSIAL DAN INTEGRAL

DIFERENSIAL/TURUNAN

Bila posisi

r = tⁿ

maka persamaan kecepatan

v = dr/dt

v = d(tⁿ)/dt

v = n.t^n-1

Demikian pula bila, kecepatan

v = 2tⁿ

maka persamaan percepatan

a = dv/dt

a = d(2.tn)/dt

a = 2.nt^n-1

INTEGRAL

Bila percepatan

a = tⁿ

maka persamaan kecepatan

v = ∫ a dt

v = ∫ tⁿ dt

v = (1/(n+1))x t ⁿ⁺¹ + c

Hukum Newton

HUKUM NEWTON I

HUKUM NEWTON I disebut juga hukum kelembaman (Inersia).
Sifat lembam benda adalah sifat mempertahankan keadaannya, yaitu keadaan tetap diam atau keaduan tetap bergerak beraturan.

DEFINISI HUKUM NEWTON I :
Setiap benda akan tetap bergerak lurus beraturan atau tetap dalam keadaan diam jika tidak ada resultan
gaya (F) yang bekerja pada benda itu, jadi:

S F = 0 a = 0 karena v=0 (diam), atau v= konstan (GLB)

HUKUM NEWTON II

a = F/m

S F = m a

S F = jumlah gaya-gaya pada benda
m = massa benda
a = percepatan benda

Rumus ini sangat penting karena pada hampir semna persoalan gerak {mendatar/translasi (GLBB) dan melingkar (GMB/GMBB)} yang berhubungan dengan percepatan den massa benda dapat diselesaikan dengan rumus tersebut.

HUKUM NEWTON III

DEFINISI HUKUM NEWTON III:

Jika suatu benda mengerjakan gaya pada benda kedua maka benda kedua tersebut mengerjakan juga gaya pada benda pertama, yang besar gayanya = gaya yang diterima tetapi berlawanan arah. Perlu diperhatikan bahwa kedua gaya tersebut harus bekerja pada dua benda yang berlainan.

F _aksi = - F _reaksi

N dan T₁= aksi reaksi (bekerja pada dua benda)

T₂ dan W = bukan aksi reaksi (bekerja pada tiga benda)

Gaya Gravitasi

Massa, Berat-Gaya Gravitasi dan Gaya Normal

Pengantar

Dalam kehidupan sehari-hari kita sering menggunakan istilah massa dan berat. Ketika mengukur badan kita dengan timbangan, kita selalu menyatakannya dengan berat. Jika ditinjau dari ilmu fisika, yang kita maksudkan sebenarnya massa, bukan berat. Pengertian massa dan berat yang kita gunakan dalam kehidupan sehari-hari sangat berbeda maknanya dalam ilmu fisika. Pada kesempatan ini kita akan belajar tentang massa dan berat. Pembahasan ini diselipkan di awal pembahasan hukum Newton, karena Hukum Newton selalu menggunakan konsep massa dan berat. Oleh karena itu sangat disarankan agar anda mempelajari pembahasan ini terlebih dahulu sebelum mempelajari Hukum Newton. Akhirnya, gurumuda mengucapkan selamat belajar… Semoga setelah mempelajari topik ini anda dapat membedakan pengertian massa dan berat dengan baik dan benar, sehingga membantu anda memahami Hukum Newton dengan mudah.

PENGERTIAN MASSA

Apa yang anda ketahui tentang massa ?

Hukum Newton yang akan kita pelajari nanti menggunakan konsep massa. Eyang Newton menggunakan konsep massa sebagai sinonim jumlah zat. Pandangan mengenai massa benda seperti ini tidak terlalu tepat karena ?jumlah zat’ tidak terdefinisi dengan baik. Dengan kata lain tidak ada cara praktis untuk menghitung partikel-partkel tersebut. Lebih tepatnya, massa merupakan ukuran inersia/kelembaman suatu benda (kemampuan mempertahankan keadaan suatu gerak). Makin besar massa suatu benda, makin sulit mengubah keadaan gerak benda tersebut. Semakin besar massa benda, semakin sulit menggerakannya dari keadaan diam, atau menghentikannya ketika sedang bergerak atau merubah gerakannya keluar dari lintasannya yang lurus. Kita dapat mengatakan bahwa semakin besar massa benda, semakin besar hambatan benda tersebut untuk dipercepat. Konsep ini dengan mudah dapat kita kaitkan dengan kehidupan sehari-hari. Jika kita memukul bola tenis meja dan bola basket dengan gaya yang sama maka tentu saja bola basket akan bergerak lebih lambat/bola basket memiliki percepatan yang lebih kecil dibandingkan denga bola tenis. Demikian juga sebuah truk gandeng yang sedang bergerak lebih sulit dihentikan dibandingkan dengan sebuah taxi. Jika sebuah gaya menghasilkan percepatan yang besar, maka massa benda kecil; jika gaya yang sama menyebabkan percepatan kecil, maka massa benda besar.

Satuan Sistem Internasional untuk massa adalah Kilogram (kg). Lambang massa adalah m, yang merupakan inisial dari kata mass (kata massa dalam bahasa inggris). Lambang ini merupakan ketetapan yang dibuat untuk penyeragaman. Bayangkanlah seandainya setelah menamatkan SMA di Indonesia dan anda melanjutkan belajar pada perguruan tinggi di luar negeri maka anda harus menyesuaikan lagi ilmu fisika yang pernah dipelajari di Indonesia, seandainya kita menggunakan lambang lain. Massa merupakan besaran skalar, yakni besaran yang hanya mempunyai nilai/besar saja.

PENGERTIAN BERAT

Dalam kehidupan sehari-hari kita sering menggunakan istilah massa dan berat secara keliru. Oleh karena itu kita perlu membedakan pengertian massa dan berat secara benar. Massa adalah sifat dari benda itu sendiri, yakni ukuran kelembaman benda tersebut atau “jumlah zat’-nya. Sedangkan berat adalah gaya, gaya gravitasi yang bekerja pada sebuah benda. Untuk melihat perbedaannya, misalnya kita membawa sebuah benda ke bulan. Jika kita tidak akan pernah ke bulan, benda tersebut kita titipkan saja lewat para astronout ketika berada di bulan, berat benda tersebut hanya seperenam dari beratnya di bumi karena gaya gravitasi di bulan enam kali lebih kecil dibandingkan dengan gaya gravitasi di bumi. Tetapi massa benda tersebut tetap sama. Benda tersebut tetap memiliki jumlah zat yang sama dan inersia alias kelembamannya juga sama. Sebuah batu ketika dibawa ke bulan, tetap menjadi batu dengan ukuran yang sama. Yang berbeda adalah berat-nya alias gaya gravitasi yang bekerja pada batu tersebut.

Secara matematis, berat di tulis sebagai berikut :

w = m g

w adalah inisial dari weight (kata berat dalam bahasa Inggris). m adalah lambang massa dan g adalah lambang gaya gravitasi. Jadi secara matematis, w adalah hasil kali antara massa dan gravitasi. massa adalah besaran skalar, sedangkan gravitasi adalah besaran vektor. Perkalian antara skalar (massa) dengan vektor (gravitasi), menghasilkan besaran vektor (Berat). Jika anda kebingungan, silahkan pelajari kembali pembahasan mengenai perkalian antara besaran vektor dan skalar. Dengan demikian Berat termasuk besaran vektor (besaran vektor adalah besaran yang memiliki besar dan arah). Arah Berat sama dengan arah gravitasi, yakni menuju ke pusat bumi alias tegak lurus ke bawah (permukaan tanah).

Vektor berat benda selalu digambarkan berarah tegak lurus ke bawah, di manapun posisi benda diletakan, baik pada bidang horisontal, bidang miring, atau pada bidang tegak. Perhatikan gambar di bawah.

Satuan Berat adalah kg m/s². Dari manakah asal satuan ini ? tolong ingat kembali pelajaran mengenai dimensi besaran. Itu fungsinya kita belajar dimensi (besaran dan satuan) di awal pelajaran fisika. Nama lain satuan Berat adalah Newton. Newton adalah satuan Gaya, dengan demikian secara matematis kita sudah menunjukan bahwa Berat juga termasuk Gaya.

Latihan Soal 1 :

Berapakah massa dirimu seandainya berat dirimu 400 Newton ? anggap saja gravitasi bernilai 10 m/s²

Latihan Soal 2 :

Massa Gurumuda di bumi adalah 50 kg. Berapa berat Gurumuda di bulan seandainya Gurumuda jalan-jalan ke bulan ? anggap saja percepatan gravitasi di bumi 10 m/s² dan gravitasi di bulan seperenam gravitasi di bumi.

GRAVITASI

Ada usul agar artikel atau bagian dari halaman Tarik-menarik digabungkan ke halaman atau bagian ini. (diskusikan)

Gravitasi adalah gaya tarik-menarik yang terjadi antara semua partikel yang mempunyai massa di alam semesta. Fisika modern mendeskripsikan gravitasi menggunakan Teori Relativitas Umum dari Einstein, namun hukum gravitasi universal Newton yang lebih sederhana merupakan hampiran yang cukup akurat dalam kebanyakan kasus.

Sebagai contoh, Bumi yang memiliki massa yang sangat besar menghasilkan gaya gravitasi yang sangat besar untuk menarik benda-benda disekitarnya, termasuk makhluk hidup, dan benda benda yang ada di bumi. Gaya gravitasi ini juga menarik benda-benda yang ada diluar angkasa, seperti bulan, meteor, dan benda angkasa laiinnya, termasuk satelite buatan manusia.

Beberapa teori yang belum dapat dibuktikan menyebutkan bahwa gaya gravitasi timbul karena adanya partikel gravitron dalam setiap atom.

Hukum Gravitasi Universal Newton

Hukum gravitasi universal Newton dirumuskan sebagai berikut:

Setiap massa titik menarik semua massa titik lainnya dengan gaya segaris dengan garis yang menghubungkan kedua titik. Besar gaya tersebut berbanding lurus dengan perkalian kedua massa tersebut dan berbanding terbalik dengan kuadrat jarak antara kedua massa titik tersebut.

$F = G \frac{m_1 m_2}{r^2}$

F adalah besar dari gaya gravitasi antara kedua massa titik tersebut

G adalah konstanta gravitasi

m₁ adalah besar massa titik pertama

m₂ adalah besar massa titik kedua

r adalah jarak antara kedua massa titik

Dalam sistem Internasional, F diukur dalam newton (N), m₁ dan m₂ dalam kilograms (kg), r dalam meter (m), dsn konstanta G kira-kira sama dengan 6,67 × 10⁻¹¹ N m² kg⁻².

Dari persamaan ini dapat diturunkan persamaan untuk menghitung Berat. Berat suatu benda adalah hasil kali massa benda tersebut dengan percepatan gravitasi bumi. Persamaan tersebut dapat dituliskan sebagai berikut: $W = m g$ . W adalah gaya berat benda tersebut, m adalah massa dan g adalah percepatan gravitasi. Percepatan gravitasi ini berbeda-beda dari satu tempat ke tempat lain.

Percepatan gravitasi di permukaan bumi secara rata-rata bernilai 9,8 m/s². kenyataannya, nilai gravitasi (g) sedikit berubah dari satu titik ke titik lain di permukaan bumi, dari kira-kira 9, 78 m/s² sampai 9,82 m/s². beberapa faktor yang mempengaruhi hal tersebut antara lain : pertama, bumi kita tidak benar-benar bulat, percepatan gravitasi bergantung pada jaraknya dari pusat bumi (planet); kedua, percepatan gravitasi tergantung dari jaraknya terhadap permukaan bumi. Semakin tinggi sebuah benda dari permukaan bumi, semakin kecil percepatan gravitasi; ketiga, percepatan gravitasi bergantung pada planet tempat benda berada, di mana setiap planet, satelit atau benda angkasa lainnya memiliki gravitasi yang berbeda.

Mengapa Gravitasi di permukaan bumi berbeda-beda ? mengapa percepatan gravitasi di setiap planet berbeda ? untuk mengetahui hal ini, anda perlu mengetahui apa sebenarnya gravitasi atau apa yang membuat bumi dan benda angkasa lainnya, termasuk bulan memiliki gravitasi. Mengenai hal ini selengkapnya akan kita pelajari pada pokok bahasan teori relativitas umum eyang Einstein. Pada kesempatan ini Gurumuda ingin menjawab rasa penasaran anda, seandainya anda ingin mengetahui apa itu gravitasi sesungguhnya sehingga setiap benda selalu jatuh ke permukaan bumi.

Untuk memudahkan pemahaman anda mengenai gravitasi, bayangkanlah anda dan teman dekat atau pacar anda yang cantik+ merentangkan sebuah kain (sebaiknya kain tersebut terbuat dari karet). Sekarang, letakan sebuah benda, dari ukuran terkecil hingga ukuran besar di atas kain atau lembaran karet tersebut. Apa yang anda amati ? jika yang anda letakan adalah sebuah kelereng, maka lekukan yang terbentuk kecil, tetapi jika anda meletakan sebongkah batu yang berukuran besar maka lekukan pada kain atau lembaran karet tersebut sangat besar. nah, sekarang, letakan sebuah kerikil atau batu kecil pada pinggir kain tersebut. Apa yang anda amati ? kerikil atau batu kecil tersebut akan terperosok alias jatuh menuju pusat lekukan, di mana batu besar yang anda letakan pada kain berada. Setiap benda angkasa yang bermassa (termasuk bumi) selalu membuat lekukan dalam ruang waktu. hal ini yang menyebabkan setiap benda seolah-olah ditarik bumi atau benda angkasa lainnya. Sebenarnya ini disebabkan oleh efek lekukan, sebagaimana ilustrasi kain karet dan batu di atas. Selengkapnya anda pelajari pada pembahasan mengenai Teori Relativitas Umum (kelas XII).

Pada pembahasan mengenai Gerak Jatuh Bebas, kita telah belajar bahwa benda-benda yang dijatuhkan dekat permukaan bumi akan jatuh dengan percepatan yang sama, g (percepatan gravitasi), seandainya hambatan udara diabaikan. Gaya yang menyebabkan percepatan ini disebut gaya gravitasi. Gaya gravitasi bekerja pada sebuah benda ketika benda tersebut jatuh.

Kita terapkan hukum II Newton untuk gaya gravitasi dan untuk percepatan a, kita ganti dengan percepatan gravitasi (g). ingat kembali pelajaran Gerak Jatuh Bebas. Benda yang jatuh hanya dipengaruhi oleh percepatan gravitasi. Dengan demikian Gaya Gravitasi yang pada sebuah benda, F_G, yang besarnya disebut berat, dapat ditulis sebagai :

F_G= mg

Arah gaya ini ke bawah, menuju ke pusat bumi. Persamaan ini sama dengan w = mg, seperti yang sudah kita pelajari di atas, karena berat adalah gaya gravitasi yang bekerja pada sebuah benda.

Ketika benda berada dalam keadaan diam di permukaan bumi, gaya gravitasi yang ada pada benda tersebut tidak hilang. Untuk membuktikaan hal ini, kita bisa mengukur benda tersebut dengan neraca pegas dan membandingkannya dengan hasil perhitungan kita (F_G = m g atau w = mg). Lalu mengapa benda tidak bergerak ? Dari hukum II Newton, gaya total untuk benda yang diam adalah nol. Jika demikian, pasti ada gaya lain yang bekerja pada benda tersebut, untuk mengimbangi gaya gravitasi. Gaya apakah itu ?

GAYA NORMAL

Ketika kita meletakan sebuah kotak di atas meja, berat kotak tersebut menekan meja ke bawah dan sebaliknya meja membalas dengan memberikan gaya ke atas (lihat gambar di bawah). Gaya yang diberikan oleh meja bisa disebut gaya kontak, karena gaya tersebut terjadi karena adanya sentuhan antara kotak dan meja. Sebuah gaya kontak yang tegak lurus terhadap permukaan kontak disebut Gaya Normal (normal berarti tegak lurus), dan mempunyai Lambang F_Natau bisa ditulis N.

Kedua gaya yang ditunjukkan pada gambar diatas bekerja pada kotak sehingga kotak tetap diam. Selisih kedua gaya tersebut (gaya total) pasti nol, sehinga kotak tersebut diam/tidak jatuh ke tanah. F_Gatauw dan N pasti memiliki besar yang sama dan memiliki arah yang berlawanan, sehingga gaya total atau selisih kedua gaya tersebut nol. Gaya-gaya tersebut bukan gaya aksi reaksi yang dijelaskan pada Hukum III Newton. Ingat bahwa gaya aksi reaksi bekerja pada benda yang berbeda, sedangkan kedua gaya di atas (Gaya berat dan Gaya Normal) bekerja pada benda yang sama, yakni kotak. Perhatikan gambar di atas secara saksama. Gaya berat benda yang menekan meja digambarkan pada titik pusat kotak alias berada di tengah-tengah kotak. Sedangkan Gaya Normal digambarkan pada permukaan sentuh antara kotak dan meja.

Lalu apa gaya reaksinya ? gaya ke atas yang diberikan oleh meja terhadap kotak adalah N, disebut gaya aksi. Gaya reaksi diberikan oleh kotak kepada meja, yakni N’, sebagaimana diperlihatkan pada gambar di bawah. Perhatikan baik-baik posisi tanda panah pada gambar. Tanda panah yang mewakili N’ digambarkan pada meja, bukan pada kotak. Panjang tanda panah sama, hal ini menunjukkan bahwa besarnya gaya sama, hanya berlawanan arah (aksi = – reaksi). Mengenai aksi-reaksi selengkapnya dipelajari pada Pokok Bahasan Hukum III Newton.

Gaya Normal (N) bekerja pada bidang sentuh antara dua benda yang saling bersentuhan dan arahnya selalu tegak lurus pada bidang sentuh. Beberapa contoh arah Gaya Normal terhadap gaya sentuh ditunjukkan pada gambar di bawah.

Contoh Soal 1 :

Sebuah buku diletakkan di atas sebuah meja yang permukaannya datar sebagaimana ditunjukkan pada gambar di bawah. Apabila massa buku 1 kg, berapakah Gaya Normal (N) yang diberikan meja terhadap buku ? anggap saja gravitasi 10 m/s²

Soal ini ma gampang

Dikerjain sendiri ya ? masa ga bisa….. tinggal masuk’n rumus aja.

Contoh Soal 2 :

Sebuah balok diletakkan di atas sebuah papan yang diletakkan miring sebagaimana ditunjukkan pada gambar di bawah. Apabila massa balok 5 kg dan sudut yang dibentuk antara papan dengan lantai adalah 45^o, berapakah Gaya Normal (N) yang diberikan meja terhadap buku ? anggap saja gravitasi 10 m/s²

Soal kaya gini ma gampang. Kerjain sendiri ya ?

Panduan Jawaban :

baGaImaNa MeNgGeRJakAnnYa-kaH ?

Karena balok terletak pada bidang miring maka kita tidak bisa menghitung N seperti contoh soal 1. cermati gambar di bawah.

Referensi :

Giancoli, Douglas C., 2001, Fisika Jilid I (terjemahan), Jakarta : Penerbit Erlangga

Halliday dan Resnick, 1991, Fisika Jilid I, Terjemahan, Jakarta : Penerbit Erlangga

Tipler, P.A.,1998, Fisika untuk Sains dan Teknik-Jilid I (terjemahan), Jakarta : Penebit Erlangga

Young, Hugh D. & Freedman, Roger A., 2002, Fisika Universitas (terjemahan), Jakarta : Penerbit Erlangga

Gaya Gesek

Gaya Gesekan – Gesekan Statis dan Kinetis

Pengantar

Pernahkah anda jatuh terpeleset karena menginjak sesuatu yang licin ? jika belum, silahkan mencoba kita bisa terpeleset ketika menginjakkan kaki pada sesuatu yang licin karena tidak ada gaya gesek yang bekerja. Tanpa gaya gesek, kita tidak akan bisa berjalan, roda sepeda motor atau mobil juga tidak akan bisa berputar, demikian juga pesawat terbang akan selalu tergelincir. Masa sich ? berita di televisi dan surat kabar yang mengatakan bahwa pesawat terbang tergelincir merupakan salah satu bukti, demikian juga ketika anda terpeleset dan jatuh sambil tertawa. Kehidupan kita sehari-hari tidak terlepas dari bantuan gaya gesekan, walaupun terkadang tidak kita sadari. Pada kesempatan ini gurumuda akan membantu anda untuk mengenal lebih jauh Gaya Gesekan. Dalam pembahasan mengenai hukum Newton, kita akan selalu berhubungan dengan gaya gesekan. Oleh karena itu, pahamilah konsep Gaya Gesekan dengan baik sehingga anda bisa memahami Hukum Newton dengan lebih mudah. Selamat belajar, semoga sukses…

KONSEP GAYA GESEKAN

Gesekan biasanya terjadi di antara dua permukaan benda yang bersentuhan, baik terhadap udara, air atau benda padat. Ketika sebuah benda bergerak di udara, permukaan benda tersebut akan bersentuhan dengan udara sehingga terjadi gesekan antara benda tersebut dengan udara. Demikian juga ketika bergerak di dalam air. Gaya gesekan juga selalu terjadi antara permukaan benda padat yang bersentuhan, sekalipun benda tersebut sangat licin. Permukaan benda yang sangat licin pun sebenarnya sangat kasar dalam skala mikroskopis. Ketika kita mencoba menggerakan sebuah benda, tonjolan-tonjolan miskroskopis ini mengganggu gerak tersebut. Sebagai tambahan, pada tingkat atom (ingat bahwa semua materi tersusun dari atom-atom), sebuah tonjolan pada permukaan menyebabkan atom-atom sangat dekat dengan permukaan lainnya, sehingga gaya-gaya listrik di antara atom dapat membentuk ikatan kimia, sebagai penyatu kecil di antara dua permukaan benda yang bergerak. Ketika sebuah benda bergerak, misalnya ketika kita mendorong sebuah buku pada permukaan meja, gerakan buku tersebut mengalami hambatan dan akhirnya berhenti, karena terjadi gesekan antara permukaan bawah buku dengan permukaan meja serta gesekan antara permukaan buku dengan udara, di mana dalam skala miskropis, hal ini terjadi akibat pembentukan dan pelepasan ikatan tersebut.

Jika permukaan suatu benda bergeseran dengan permukaan benda lain, masing-masing benda tersebut melakukan gaya gesekan antara satu dengan yang lain. Gaya gesekan pada benda yang bergerak selalu berlawanan arah dengan arah gerakan benda tersebut. Selain menghambat gerak benda, gesekan dapat menimbulkan aus dan kerusakan. Hal ini dapat kita amati pada mesin kendaraan. Misalnya ketika kita memberikan minyak pelumas pada mesin sepeda motor, sebenarnya kita ingin mengurangi gaya gesekan yang terjadi di dalam mesin. Jika tidak diberi minyak pelumas maka mesin kendaraan kita cepat rusak. Contoh ini merupakan salah satu kerugian yang disebabkan oleh gaya gesek.

Kita dapat berjalan karena terdapat gaya gesek antara permukaan sandal atau sepatu dengan permukaan tanah. Jika anda tidak biasa menggunakan alas kaki gaya gesek tersebut bekerja antara permukaan bawah kaki dengan permukaan tanah atau lantai. Alas sepatu atau sandal biasanya kasar / bergerigi alias tidak licin. Para pembuat sepatu dan sandal membuatnya demikian karena mereka sudah mengetahui konsep gaya gesekan. Demikian juga alas sepatu bola yang dipakai oleh pemain sepak bola, yang terdiri dari tonjolan-tonjolan kecil. Apabila alas sepatu atau sandal sangat licin, maka anda akan terpeleset ketika berjalan di atas lantai yang licin atau gaya gesek yang bekerja sangat kecil sehingga akan mempersulit gerakan anda. Ini merupakan contoh gaya gesek yang menguntungkan.

Ketika sebuah benda berguling di atas suatu permukaan (misalnya roda kendaraan yang berputar atau bola yang berguling di tanah), gaya gesekan tetap ada walaupun lebih kecil dibandingkan dengan ketika benda tersebut meluncur di atas permukaan benda lain. Gaya gesekan yang bekerja pada benda yang berguling di atas permukaan benda lainnya dikenal dengan gaya gesekan rotasi. Sedangkan gaya gesekan yang bekerja pada permukaan benda yang meluncur di atas permukaan benda lain (misalnya buku yang didorong di atas permukaan meja) disebut sebagai gaya gesekan translasi. Pada kesempatan ini kita hanya membahas gaya gesekan translasi, yaitu gaya gesekan yang bekerja pada benda padat yang meluncur di atas benda padat lainnya.

GAYA GESEKAN STATIK DAN KINETIK

Lakukanlah percobaan berikut ini untuk menambah pemahaman anda. Letakanlah sebuah balok pada permukaan meja. Ikatlah sebuah neraca pegas (alat untuk mengukur besar gaya) pada sisi depan balok tersebut. Sekarang, tarik pegas perlahan-lahan sambil mengamati perubahan skala pada neraca pegas. Tampak bahwa balok tidak bergerak jika diberikan gaya yang kecil. Balok belum bergerak karena gaya tarik yang kita berikan pada balok diimbangi oleh gaya gesekan antara alas balok dengan permukaan meja. Ketika balok belum bergerak, besarnya gaya gesekan sama dengan gaya tarik yang kita berikan. Jika tarikan kita semakin kuat, terlihat bahwa pada suatu harga tertentu balok mulai bergerak. Pada saat balok mulai bergerak, gaya yang sama menghasilkan gaya dipercepat. Dengan memperkecil kembali gaya tarik tersebut, kita dapat menjaga agar balok bergerak dengan laju tetap; tanpa percepatan. Kita juga bisa mempercepat gerak balok tersebut dengan menambah gaya tarik.

Gaya gesekan yang bekerja pada dua permukaan benda yang bersentuhan, ketika benda tersebut belum bergerak disebut gaya gesek statik (lambangnya f_s). Gaya gesek statis yang maksimum sama dengan gaya terkecil yang dibutuhkan agar benda mulai bergerak. Ketika benda telah bergerak, gaya gesekan antara dua permukaan biasanya berkurang sehingga diperlukan gaya yang lebih kecil agar benda bergerak dengan laju tetap. Ketika benda telah bergerak, gaya gesekan masih bekerja pada permukaan benda yang bersentuhan tersebut. Gaya gesekan yang bekerja ketika benda bergerak disebut gaya gesekan kinetik (lambangnya f_k) (kinetik berasal dari bahasa yunani yang berarti “bergerak”). Ketika sebuah benda bergerak pada permukaan benda lain, gaya gesekan bekerja berlawanan arah terhadap kecepatan benda. Hasil eksperimen menunjukkan bahwa pada permukaan benda yang kering tanpa pelumas, besar gaya gesekan sebanding dengan Gaya Normal.

KOOFISIEN GESEKAN STATIK DAN KINETIK

Perhatikan bahwa hubungan antara gaya normal dan gaya gesekan pada persamaan di atas hanya untuk besarnya saja. Arah kedua gaya tersebut selalu saling tegak lurus satu dengan yang lain, sebagaimana diperlihatkan pada gambar di bawah ini. Berikut ini keterangan untuk gambar di bawah : f_kadalah gaya gesekan kinetik, f_sadalah gaya gesekan statik, F adalah gaya tarik, N adalah gaya normal, w adalah gaya berat, m adalah massa, g adalah percepatan gravitasi.

Contoh Soal 1 :

Sebuah buku berada dalam keadaam diam di atas meja yang permukaannya datar. Koofisien gesekan statik adalah 0,4 dan koofisien gesekan kinetik adalah 0,30. Jika massa buku tersebut adalah 1 kg, berapakah Gaya minimum yang diberikan agar buku itu mulai bergerak ? anggap saja percepatan gravitasi (g) = 10 m/s²

Panduan Jawaban :

Terlebih dahulu kita hitung besar Gaya Normal (N).

N = w = m g = (1 kg) (10 m/s²) = 10 kg m/s² = 10 N.

Setelah memperoleh besar Gaya Normal, selanjutnya kita hitung besar gaya gesek statis (fs).

Besar gaya gesek statis adalah 4 N. Agar buku dapat bergerak, maka gaya tarik minimum yang diberikan harus lebih besar dari 4 Newton (agar benda mulai bergerak maka F > fs)

Contoh Soal 2 :

Sebuah balok bermassa 10 kg diletakkan pada bidang miring sebagaimana tampak pada gambar di bawah. Jika sudut yang dibentuk antara bidang miring dengan permukaan lantai sebesar 30^o dan koofisien gesekan kinetik adalah 0,4, berapakah gaya gesekan kinetis yang bekerja pada permukaan balok dan bidang miring ?

Panduan Jawaban

Referensi :

Giancoli, Douglas C., 2001, Fisika Jilid I (terjemahan), Jakarta : Penerbit Erlangga

Halliday dan Resnick, 1991, Fisika Jilid I, Terjemahan, Jakarta : Penerbit Erlangga

Tipler, P.A.,1998, Fisika untuk Sains dan Teknik-Jilid I (terjemahan), Jakarta : Penebit Erlangga

Young, Hugh D. & Freedman, Roger A., 2002, Fisika Universitas (terjemahan), Jakarta : Penerbit Erlangga

Hukum Kepler

Pengantar

Sebelum kita mempelajari hukum Kepler secara lebih mendalam, terlebih dahulu kita kenang kembali kisah masa lalu yang mengantar Paman Kepler merumuskan hukumnya yang terkenal sampai di seluruh pelosok negeri, bahkan sampai ke seluruh penjuru ruangan kelas XI IPA. Tulisan ini juga menyinggung masa lalu ilmu astronomi, sebuah kisah perkembangan ilmu pengetahuan yang selalu menuai pertentangan di tahap awal perkembangannya.

Sejarah Panjang

Awal perkembangan ilmu astronomi modern dimulai oleh Purbach (1423-1461) di universitas Wina serta lebih khusus lagi oleh muridnya Yohanes muller (1436-1476). Johanes Muller pergi ke Italia khusus untuk belajar karya asli Ptolemeus tentang astronomi bersama temannya Walther (1430-1504). Walther adalah seorang yang kaya, ia memiliki observatorium pribadi, serta mesin percetakan pribadi. Muller bersama Walther membuat penanggalan berdasarkan benda-benda langit yang banyak dipakai oleh para pelaut Spanyol dan Portugis. Muller kemudian pergi ke Roma untuk melakukan pembaruan kalender di sana, akan tetapi ia meninggal sebelum dapat melaksanakan niatnya. Pengamatan muller dilanjutkan oleh temannya, Walther dan Albrecht Durer. Maka, ketika Nicolas Copernicus (1473-1543) memulai karyanya, telah terdapat cukup banyak karya hasil pengamatan astronomi.

Sistem Copernicus yang baru tentang alam semesta menempatkan matahari sebagai pusat alam semesta, serta terdapat tiga jenis gerakan bumi. Tiga jenis gerakan bumi itu adalah gerak rotasi bumi (perputaran bumi pada porosnya), gerak revolusi (gerak bumi mengelilingi matahari) dan suatu girasi perputaran sumbu bumi yang mempertahankan waktu siang dan malam sama panjangnya. Teori Copernicus tersebut ditulis tangan dan diedarkan di antara kawan-kawannya pada tahun 1530. Teori Copernicus menjadi semakin terkenal dan menarik perhatian seorang ahli matematika dari wittenberg bernama George Rheticus (1514-1576). Rheticus kemudian belajar bersama Copernicus dan pada tahun 1540 menerbitkan buku tentang teori Copernicus. Akhirnya Copernicus menerbitkan hasil karyanya sendiri pada tahun 1543 berjudul On the Revolutions Of the Celestial Orbs.

Buku copernicus dicetak di Nuremberg, pada awalnya di bawah supervisi Rheticus, kemudian dilanjutkan di bawah supervisi Andreas Osiander, seorang pastor Lutheran. Osiander menambahkan kata pengantar untuk karya Copernicus dengan menyatakan bahwa teori yang baru itu tidak harus benar, dan dapat dipandang semata-mata sebagai suatu kecocokan metode matematis tentang benda-benda langit. Copernicus sendiri tidak berpendapat begitu. Ia berpendapat bahwa sistem semesta yang dikemukakannya adalah nyata.

Copernicus berpendapat bahwa sistem yang dikemukakan oleh ptolemous ‘tidak cukup tepat, tidak cukup memuaskan pikiran’, karena ptolemous beranjak langsung dari karya kelompok Pythagoras. Untuk menjelaskan gerakan benda-benda langit, ptolemous menganggap bahwa benda-benda langit itu bergerak melingkar dengan kecepatan angular yang tidak sama relatif terhadap pusatnya, kecepatan anguler itu hanya sama terhadap titik di luar pusat lingkaran itu. Menurut copernicus, asumsi itu merupakan kesalahan pokok dari sistem ptolemous. Akan tetapi hal ini bukan hal pokok yang dikemukakan oleh copernicus. Kritik utama yang dikemukakan oleh copernicus kepada para ahli astronomi pendahulunya adalah, dengan menggunakan aksioma-aksiomanya, mereka telah gagal menjelaskan gerakan benda-benda langit yang teramati dan juga teori-teori yang mereka kembangkan melibatkan sistem yang rumit yang tidak perlu. Copernicus menilai para pendahulunya dengan mengatakan : “di dalam metode yang dikembangkan, mereka telah mengabaikan hal-hal penting atau menambahkan hal-hal yang tidak perlu”.

Copernicus memusatkan perhatian pada hal yang terakhir. Ia melihat bahwa para leluhurnya telah menambahkan tiga gerakan bumi untuk setiap benda langit agar sampai pada kesimpulan bahwa bumi berada diam di pusat putaran. Ketiga lingkaran tersebut telah ditambahkan untuk setiap benda langit di dalam sistem geometris bangsa Yunani untuk menjelaskan gerakan benda-benda langit dengan bumi sebagai pusatnya. Copernicus berpendapat bahwa lingkaran-lingkaran tersebut tidak diperlukan dengan berpendapat bahwa bumi berputar pada sumbuhnya setiap hari dan bergerak melintasi orbitnya mengitari matahari setiap tahun. Dengan cara demikian, Copernicus mengurangi jumlah lingkaran yang diperlukan untuk menjelaskan gerakan benda-benda langit.

Dengan sistem yang dikemukakannya itu, Copernicus memberikan jawaban yang paling sederhana untuk menjawab pertanyaan yang diajukan bangsa Yunani tentang bagaimana menjelaskan gerakan benda-benda langit dalam suatu gerakan yang melingkar dan seragam. Tidak ada hal yang baru dalam metode tersebut, hal itu telah dipergunakan oleh para astronom sejak jaman Pythagoras. Dengan menggunakan konsepsi yang dipakai oleh Pythagoras, ia mencampakkan sistem yang dikembangkan oleh bangsa yunani. Akan tetapi, ada satu konsep yang tidak dipakainya, yaitu bahwa benda-benda langit adalah mulia.

Di dalam sistem Copernicus, bumi berputar mengitari matahari, seperti planet-planet lainnya. Bumi menjalani gerakan yang seragam dan melingkar sebagai benda langit, suatu gerakan yang sejak lama diyakini sebagai gerakan yang sempurna. Lebih jauh, copernicus menekankan kesamaan antara bumi dengan benda-benda langit lainnya bahwa semuanya memiliki gravitasi. Gravitasi ini tidak berada di langit, melainkan bekerja pada materi, seperti bumi dan benda-benda langit memiliki gaya ikat dan mempertahankannya dalam suatu lingkaran yang sempurna. Untuk hal ini penjelasan copernicus agak berbau teologis : “menurut saya gravitasi tidak lain daripada suatu kekuatan alam yang diciptakan oleh pencipta agar supaya semuanya berada dalam kesatuan dan keutuhan. Kekuatan seperti itu mungkin juga dimiliki oleh matahari, bulan dan planet-planet agar semuanya tetap bundar”

Sistem copernicus lebih bagus dan lebih sederhana daripada sistem ptolomeus. Di dalam sistem lama, benda-benda langit memiliki baik gerakan timur-barat maupun rotasi pada arah yang berlawanan. Dalam sistem copernicus, bumi dan semua planet bergerak mengitari matahari dengan arah yang sama dan laju yang berkurang semakin jauh dari matahari. Sementara itu, matahari yang berada di pusat dan bintang-bintang yang berada di luar tatasurya berada pada tempatnya yang tetap. Sekarang dapat dijelaskan mengapa planet-planet kelihatan mendekati dan menjahui bumi. Planet-planet itu pada suatu saat berada pada satu sisi yang sama dengan bumi, tetapi pada saat yang lain berada pada sisi yang berseberangan

Dengan sistem Copernicus, perhitungan astronomi dibuat menjadi lebih mudah, karena melibatkan jumlah lingkaran yang lebih sedikit. Tetapi prakiraan posisi planet-planet dan perhitungan lainnya tidak lebih tepat daripada dihitung dengan menggunakan sistem ptolemous, keduanya masih memiliki kesalahan sekitar satu persen. Selanjutnya terdapat keberatan-keberatan terhadap sistem Copernicus. Pertama, dan mungkin tidak terlalu serius ketika itu, adalah kenyataan bahwa pusat tata surya tidak tepat berada pada matahari. Copernicus menempatkan pusat tatasurya pada pusat orbit bumi, yang tidak persis berada pada matahari, untuk menjelaskan perbedaan panjang musim-musim. Beberapa filsuf berpendapat bahwa pusat tata surya haruslah berada pada suatu obyek nyata, meskipun banyak juga yang menerima bahwa titik geometris dapat dipakai sebagai pusat tatasurya. Selanjutnya, para pendukung aristoteles berpendapat bahwa gravitasi bekerja ke arah titik geometris tersebut, sebagai pusat tatasurya, yang tidak harus sama dengan pusat bumi.

Keberatan kedua, yang lebih serius, menyatakan bahwa bila bumi berputar, maka udara cenderung tertinggal di belakang, hal ini akan menimbulkan angin yang arahnya ke timur. Copernicus memberikan dua jawaban untuk keberatan timur. Pertama, yang merupakan suatu jenis penjelasan abad pertengahan, yaitu udara berputar bersama-sama dengan bumi karena udara berisi partikel-partikel bumi yang memiliki sifat-sifat yang sama dengan bumi. Maka bumi menarik udara berputar bersama-sama dengan bumi karena udara bersisi partikel-partikel bumi. Maka bumi menarik udara berputar dengan bumi. Jawaban kedua yang bersifat modern, udara berputar tanpa hambatan karena udara berdampingan dengan bumi yang terus menerus berputar. Keberatan yang sama adalah apabila sebuah batu dilemparkan ke atas maka batu itu akan tertinggal oleh bumi yang berputar, sehingga kalau batu itu jatuh akan berada di sebelah barat proyeksi batu itu. Untuk keberatan ini, copernicus menjawab ‘karena benda-benda yang ditarik ke tanah oleh beratnya adalah terbuat dari tanah, maka tidak diragukan bahwa benda-benda itu memiliki sifat yang sama dengan bumi secara keseluruhan, sehingga berputar bersama-sama dengan bumi’

Keberatan lebih jauh terhadap sistem copernicus adalah bila bumi berputar, maka bumi akan hancur berkeping-keping oleh gaya sentrifugal. Copernicus menjawab bahwa bila bumi tidak berputar maka bola yang lebih besar yang ditempati oleh bintang-bintang pasti bergerak dengan kecepatan yang sangat besar dan lebih rentan oleh pengaruh gaya sentrifugal.

Nampaknya copernicus tidak menerima teori aristoteles juga tidak menerima teori adanya gaya dorong. Copernicus berpendapat bahwa spin dan gerakan dalam suatu lingkaran adalah gerakan-gerakan yang spontan, merupakan sifat alami dari suatu bentuk bola dimana bumi dan benda-benda langit ada. Oleh karena itu, copernicus tidak menggunakan hirarki para malaikat untuk menggerakan benda-benda langit, yaitu malaikat yang lebih berkuasa menggerakan benda yang lebih tinggi hirarkinya. Menurut copernicus benda-benda langit bergerak secara spontan.

Maka bersama copernicus muncul suatu sistem cosmos yang betul-betul baru. Penggerak alam semesta tidak lagi penting. Matahari sebagai pusat tatasurya menjadi pengatur alam semesta.

Terdapat figur perantara di antara pendukung aristoteles yang mendukung adanya penggerak alam semesta dan copernicus yang menyatakan matahari sebagai pusat tatasurya yaitu nicolas Cusa.

Kiranya dapat dikatakan bahwa copernicus berusaha mempromosikan suatu nilai baru dengan sistem yang dikemukakannya. Karena apabila ia sekedar ingin mengembangkan suatu sistem yang lebih sederhana, terdapat suatu sistem yang dipakai oleh tycho brahe (1546-1601). Di dalam sistem itu planet-planet berputar mengelilingi matahari, sementara itu matahari bersama-sama dengan planet-planet yang mengelilinginya sebagai satu kesatuan, berputar mengelilingi bumi yang diam yang berada pada pusat semesta. Sistem itu secara matematis ekuivalen dengan sistem copernicus, dan juga sistem itu tidak menimbulkan persoalan fisis. Tetapi sistem itu tetap mempertahankan nilai-nilai lama dalam sistem cosmos yaitu bumi sebagai pusat alam semesta. Itulah mungkin sebabnya copernicus mengajukan suatu sistem baru, heliosentris.

Dalam seluruh hidupnya, Copenicus menganut pandangan bangsa yunani bahwa gerakan benda-benda langit adalah melingkar dengan kecepatan tetap, maka meskipun sistem yang dibuat copernicus lebih sederhana dibandingkan dengan sistem ptolomeus, tetapi tetap rumit dibandingkan dengan sistem Kepler (1571-1630). Copernicus menjelaskan gerakan benda-benda langit dengan menggunakan tiga puluh empat lingkaran, sementara itu kepler hanya menggunakan tujuh elips. Seperti dikatakan oleh kepler, copernicus tidak menyadari akan adanya suatu bangunan yang sangat baik yang ada dalam genggamannya. Copernicus mengetahui bahwa gabungan beberapa lingkaran dapat menghasilkan elips, akan tetapi ia tidak pernah menggunakan elips untuk menggambarkan benda-benda langit. Lagipula, pada tahap-tahap awal, copernicus sangat menghargai hasil observasi bangsa kuno. Copernicus menentang werner yang menyatakan bahwa hasil-hasil pengamatan terakhir lebih cocok dengan sistem ptolemous daripada dengan sistem copernicus. Kenyataannya memang tiga kali lebih tepat.

Pengamatan paling penting dalam bidang astronomi modern adalah yang dilakukan oleh Ticho Brahe. Hasil pengamatan Ticho Brahe limapuluh kali lebih tepat dari hasil muller, hasil terbaik yang dapat dilakukan dengan mata telanjang. Tycho Brahe adalah orang Denmark terhormat. Raja Frederick II dari Denmark memberi tempat tinggal dan pulau Hveen untuk melakukan kegiatan astronominya. Di pulau itu Tycho Brahe membangun kastil, bengkel, percetakan pribadi, dan observatorium. Ia bekerja di pulau itu dari tahun 1576 sampai 1597. Ia berpendapat bahwa adalah tidak mungkin melakukan pengamatan tanpa panduan suatu teori. Ia menganut pendangan geosentris.

Ketika raja Frederick II wafat, fasilitas yang diterima Tycho Brahe tidak diperpanjang, kemudian Ticho Brahe pergi ke Praha pada tahun 1599, di mana ia mendapat tunjangan dari raja Rudolph II. Tahun-tahun berikutnya ia bergabung dengan astronom jerman, Johann Kepler, seorang matematikawan. Kepler adalah anak seorang tentara wurtemburg. Ia mempelajari sistem copernicus di Tubingen. Kerja sama antara Kepler dengan Ticho Brahe tidak berlangsung lama karena Ticho Brahe meninggal dunia. Setelah Ticho Brahe meninggal, Kepler tetap tinggal di Praha.

Karya pertama Kepler dalam bidang astronomi berjudul The Mysteri of the Universe yang diterbitkan pada tahun 1596. Di dalam buku itu, ia berusaha mencari suatu keselarasan antara orbit-orbit planet menurut copernicus dengan hasil pengamatan Ticho Brahe. Akan tetapi Kepler tidak berhasil menemukan keselarasan antara sistem-sistem yang dikembangkan oleh Copernicus maupun Ptolemous dengan hasil pengamatan Tycho Brahe. Oleh karena itu ia meninggalkan sistem ptolemous dan Copernicus lalu berusaha mencari sistem baru. Pada tahun 1609, Kepler menemukan ternyata elips sangat cocok dengan hasil pengamatan Ticho Brahe. Kepler tidak lagi menggunakan lingkaran sebagai lintasan benda-benda langit melainkan elips.

HUKUM KEPLER

Karya Kepler sebagian dihasilkan dari data-data hasil pengamatan yang dikumpulkan Ticho Brahe mengenai posisi planet-planet dalam geraknya di luar angkasa. Hukum ini telah dicetuskan Kepler setengah abad sebelum Newton mengajukan ketiga Hukum-nya tentang gerak dan hukum gravitasi universal. Di antara hasil karya Kepler, terdapat tiga penemuan yang sekarang kita kenal sebagai Hukum Kepler mengenai gerak planet.

Hukum I Kepler

Lintasan setiap planet ketika mengelilingi matahari berbentuk elips, di mana matahari terletak pada salah satu fokusnya.

Kepler tidak mengetahui alasan mengapa planet bergerak dengan cara demikian. Ketika mulai tertarik dengan gerak planet-planet, Newton menemukan bahwa ternyata hukum-hukum Kepler ini bisa diturunkan secara matematis dari hukum gravitasi universal dan hukum gerak Newton. Newton juga menunjukkan bahwa di antara kemungkinan yang masuk akal mengenai hukum gravitasi, hanya satu yang berbanding terbalik dengan kuadrat jarak yang konsisten dengan Hukum Kepler.

Perhatikan orbit elips yang dijelaskan pada Hukum I Kepler. Dimensi paling panjang pada orbit elips disebut sumbu mayor alias sumbu utama, dengan setengah panjang a. Setengah panjang ini disebut sumbu semiutama alias semimayor (sambil lihat gambar di bawah ya).

F₁ dan F₂ adalah titik Fokus. Matahari berada pada F₁ dan planet berada pada P. Tidak ada benda langit lainnya pada F₂. Total jarak dari F₁ ke P dan F₂ ke P sama untuk semua titik dalam kurva elips. Jarak pusat elips (O) dan titik fokus (F₁ dan F₂) adalah ea, di mana e merupakan angka tak berdimensi yang besarnya berkisar antara 0 sampai 1, disebut juga eksentrisitas. Jika e = 0 maka elips berubah menjadi lingkaran. Kenyataanya, orbit planet berbentuk elips alias mendekati lingkaran. Dengan demikian besar eksentrisitas tidak pernah bernilai nol. Nilai e untuk orbit planet bumi adalah 0,017. Perihelion merupakan titik yang terdekat dengan matahari, sedangkan titik terjauh adalah aphelion.

Pada Persamaan Hukum Gravitasi Newton, telah kita pelajari bahwa gaya tarik gravitasi berbanding terbalik dengan kuadrat jarak (1/r²), di mana hal ini hanya bisa terjadi pada orbit yang berbentuk elips atau lingkaran saja.

Contoh soal Hukum I Kepler :

Komet Halley bergerak sepanjang orbit elips mengitari matahari. Pada perihelion, komet Halley berjarak 8,75 x10⁷ km dari matahari, sedangkan pada aphelion berjarak 5,26 x 10⁹ km dari matahari. Berapakah eksentrisitas dari orbit komet halley

Panduan jawaban :

Panjang sumbu utama sama dengan total jarak komet ke matahari ketika komet berada di perihelion dan aphelion.

Panjang sumbu utama adalah 2a, dengan demikian :

Pada Perihelion, jarak komet Halley dengan matahari diperoleh dari (sambil perhatikan gambar di atas) :

a – ea = a(1-e)

Jarak komet Halley dengan matahari ketika komet Halley berada pada perihelion adalah 8,75 x10⁷ km. Dengan demikian, eksentrisitas komet Halley adalah :

Nilai eksentrisitas komet halley mendekati 1. Ini menunjukkan bahwa orbit halley sangat panjang….

Hukum II Kepler

Luas daerah yang disapu oleh garis antara matahari dengan planet adalah sama untuk setiap periode waktu yang sama.

Hal yang paling utama dalam Hukum II Kepler adalah kecepatan sektor mempunyai harga yang sama pada semua titik sepanjang orbit yang berbentuk elips.

Hukum III Kepler

Kuadrat waktu yang diperlukan oleh planet untuk menyelesaikan satu kali orbit sebanding dengan pangkat tiga jarak rata-rata planet-planet tersebut dari matahari.

Jika T₁ dan T₂ menyatakan periode dua planet, dan r₁ dan r₂ menyatakan jarak rata-rata mereka dari matahari, maka

Newton menunjukkan bahwa Hukum III Kepler juga bisa diturunkan secara matematis dari Hukum Gravitasi Universal dan Hukum Newton tentang gerak dan gerak melingkar. Sekarang mari kita tinjau Hukum III Kepler menggunakan pendekatan Newton.

Terlebih dahulu kita tinjau kasus khusus orbit lingkaran, yang merupakan kasus khusus dari orbit elips. Semoga dirimu belum melupakan Hukum Newton dan pelajaran Gerak Melingkar…

Sekarang kita masukan persamaan Hukum Gravitasi Newton dan percepatan sentripetal ke dalam persamaan Hukum II Newton :

m₁ adalah massa planet, m_M adalah massa matahari, r₁ adalah jarak rata-rata planet dari matahari, v₁ merupakan laju rata-rata planet pada orbitnya.

Waktu yang diperlukan sebuah planet untuk menyelesaikan satu orbit adalah T₁, di mana jarak tempuhnya sama dengan keliling lingkaran, 2 phi r₁. Dengan demikian, besar v₁ adalah :

Misalnya persamaan 1 kita turunkan untuk planet venus (planet 1). Penurunan persamaan yang sama dapat digunakan untuk planet bumi (planet kedua).

T₂ dan r₂ adalah periode dan jari-jari orbit planet kedua. Sekarang coba anda perhatikan persamaan 1 dan persamaan 2. Perhatikan bahwa ruas kanan kedua persamaan memiliki nilai yang sama. Dengan demikian, jika kedua persamaan ini digabungkan, akan kita peroleh :

Persamaan ini adalah Hukum III Kepler…

Kita juga bisa menurunkan persamaaan untuk menghitung besarnya periode gerak planet (T) dengan cara lain. Pertama terlebih dahulu kita turunkan untuk kasus gerak melingkar.

Sebelumnya kita telah mensubtitusikan persamaan Hukum Gravitasi Newton dan percepatan sentripetal ke dalam persamaan Hukum II Newton :

Pada pembahasan mengenai gerak melingkar beraturan, kita mempelajari bahwa laju v adalah perbandingan jarak tempuh dalam satu kali putaran (2phir) dengan periode (waktu yang dibutuhkan untuk melakukan satu kali putaran), yang secara matematis dirumuskan sebagai berikut :

Pada persamaan ini tampak bahwa periode dalam orbit lingkaran sebanding dengan pangkat 3/2 dari jari-jari orbit. Newton menunjukkan bahwa hubungan ini juga berlaku untuk orbit elips, di mana jari-jari orbit lingkaran (r) diganti dengan setengah sumbu utama a

Dibaca secara perlahan-lahan sambil direnungkan

DATA ASTRONOMI

Referensi :

Giancoli, Douglas C., 2001, Fisika Jilid I (terjemahan), Jakarta : Penerbit Erlangga

Halliday dan Resnick, 1991, Fisika Jilid I, Terjemahan, Jakarta : Penerbit Erlangga

Kanginan, Marthen, 2002, Fisika untuk SMA kelas X, Semester 1, Jakarta : Penerbit Erlangga

Tipler, P.A.,1998, Fisika untuk Sains dan Teknik-Jilid I (terjemahan), Jakarta : Penebit Erlangga

Young, Hugh D. & Freedman, Roger A., 2002, Fisika Universitas (terjemahan), Jakarta : Penerbit Erlangga

Gerak Melingkar Berubah Beraturan (GMBB)

Adalah gerak suatu benda dengan bentuk lintasan melingkar dan besar percepatan sudut/anguler (α) konstan.
Jika perecepatan anguler benda searah dengan perubahan kecepatan anguler maka perputaran benda semakin cepat, dan dikatakan GMBB dipercepat. Sebaliknya jika percepatan anguler berlawanan arah dengan perubahan kecepatan anguler benda akan semakin lambat, dan dikatakan GMBB diperlambat.

1. Percepatan Anguler (α)

Sebuah benda bergerak melingkar dengan laju anguler berubah beraturan memiliki perubahan kecepatan angulernya adalah :

Δω = ω₂ – ω₁

Dan perubahan waktu kecepatan anguler adalah Δt, maka di dapatkan :

∆ω = perubahan kecepatan sudut (rad/s)
∆t = selang waktu (s)
α = percepatan sudut/anguler (rads^-2)

Sama halnya dengan Gerak Lurus Berubah Beraturan (GLBB), pada GMBB berlaku juga :

- Mencari kecepatan sudut akhir (ω_t) :

ω_t = ω₀± α.t

- Mencari posisi sudut / besar sudut (θ) yang ditempuh:

θ= ω₀ t ± α.t²

x = R. θ

Dapat diperoleh juga :

ωt² = ω₀² ± 2 α.θ

dimana :

ωt = kecepatan sudut/anguler keadaan akhir(rad/s)
ω0 = kecepatan sudut/anguler keadaan awal (rad/s)
θ = besar sudut yang ditempuh (radian, putaran)
1 rpm = 1 putaran permenit
1 putaran = 360° = 2p rad.
x = perpindahan linier (m)
t = waktu yang diperlukan (s)
R = jari-jari lintasan (m)

2. Percepatan Tangensial (at)

Pada gerak melingkar berubah beraturan selain percepatan sentripetal (as) juga mempunyai percepatan tangensial (at).

Percepatan Tangensial (at) diperoleh :

maka : a_t = . R dengan arah menyinggung lintasan.

Partikel P memiliki komponen Percepatan :

a = a_t + a_s , dimana a_t tegak lurus a_s ( a_s a_t )

Besar Percepatan Linier Total partikel titik P :

a_t = percepatan tangensial (ms^-2)
a_s = percepatan sentripetal (ms^-2)
a = percepatan total (ms^-2)

Jika a_s = dan maka didapat :

Percepatan total (a) :

dimana

V = kelajuan linier (m/s)
R = jari-jari lintasan (m)
= percepatan sudut (rad s^-2)

Semua benda bergerak melingkar selalu memiliki percepatan sentripetal, tetapi belum tentu memiliki percepatan tangensial.

Percepatan tangensial hanya dimiliki bila benda bergerak melingkar dan mengalami perubahan kelajuan linier.

Benda yang bergerak melingkar dengan kelajuan linier tetap hanya memiliki percepatan sentripetal, tetapi tidak mempunyai percepatan tangensial (a_t = 0 ).

Contoh soal Konsep Gerak Melingkar Berubah Beraturan:
Sebuah roda mobil sedang berputar dengan kecepatan sudut 8,6 rad/s. Suatu gesekan kecil pada poros putaran menyebabkan suatu perlambatan sudut tetap sehingga akhirnya berhenti dalam waktu 192 s. Tentukan :

Percepatan sudut
Jarak yang telah ditempuh roda dari mulai bergerak sampai berhenti (jari-jari roda 20 cm)

Pembahasan :

Diketahui : ω₀= 8,6 rad/s

ω_t = 0 rad/s

t = 192 s
R = 10cm= 0,1 m

Ditanya : a.
b. x

Jawab :

= - 0,045 rads^-2

= (8,6).(192) + (-0,045).(192)²

= 826 rad

x = R.θ

= (0,1m),(826)

= 82,6 m

Ayunan Konis
Ayunan Konis (Ayunan Kerucut) adalah putaran sebuah benda yang diikat pada seutas tali yang panjangnya L ujung atas tali diikat pada satu titik tetap dan benda diputar mengitari permukaan membentuk kerucut.

Gaya yang bekerja adalah Tx sebagai gaya sentripetal yang menyebabkan benda bergerak melingkar beraturan pada bidang horizontal.
Tx = Fs

Pada Sumbu Y :
Benda tidak bergerak,maka sesuai hukum I Newton.
Fy = 0
Tcosθ – mg = 0
T cos θ = mg ....... (2)

Dari pers (1) dan (2) diperoleh :

dimana

V = kelajuan ayunan(m/s)
g = percepatan gravitasi (ms^-2)
R = jari-jari (m)
θ = besar sudut putar(rad)

Contoh soal Ayunan Konis/kerucut:
Seutas tali dengan panjang 1 m, ujung atasnya dipegang dan ujung bawah dikaitkan ke benda bermassa 100 g.Kemudian tali diputar sehingga benda bergerak melingkar horisontal dengan jari-jari lingkaran 0,5 m. Hitunglah :
a. besar tegangan tali
b. kelajuan linier benda

Pembahasan :

Diketahui : L =1 m
R = 0,5 m
m = 100g = 0,1 kg

Ditanya :
a. T
b. V

Jawab :